 学历课程
学历课程
文本一:矩形截面偏心受压构件正截面承载力的基本计算公式
6.5.1矩形截面大偏心受压构件正截面承载力计算公式
(1)计算公式
从大小偏心受压破坏特征可以看出,二者之间根本区别在于破坏时受拉钢筋能否达到屈服。这和受弯构件的适筋与超筋破坏两种情况完全一致。因此,两种偏心受压破坏形态的界限与受弯构件适筋与超筋破坏的界限也必然相同,即在破坏时纵向钢筋应力达到屈服强度,同时受压区混凝土也达到极限压应变值。
试验分析表明,大偏心受压构件,若受拉钢筋设置合适时与适筋梁相同,其受拉及受压纵向钢筋均能达到屈服强度。
由教材图6-17(b)计算图式,依据沿构件纵轴方向的内外力之和为零的平衡条件,可得:
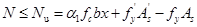 (6-24)
(6-24)
另外,依据由截面上内、外力对受拉钢筋合力点的力矩之和等于零的平衡条件,可得:
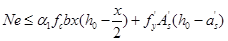 (6-25)
(6-25)
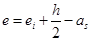 (6-26)
(6-26)
式中各参数的定义详见教材。
(2)适用条件
为了保证构件破坏时受拉区钢筋应力先达到屈服强度,要求:
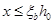 (6-27)
(6-27)
为了保证构件破坏时,受压钢筋应力能达到抗压屈服强度设计值,与双筋受弯构件相同,要求满足:
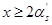 (6-28)
(6-28)
6.5.2矩形截面小偏心受压构件正截面承载力计算公式
小偏心受压构件在破坏时,靠近轴向力一侧的混凝土被压碎,受压钢筋达到屈服,而远离轴向力一侧的钢筋可能受拉也可能受压,但一般都达不到屈服强度,定义其应力值为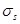 。
。
1. 远离纵向偏心力一侧的钢筋应力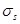 的计算公式
的计算公式
(1)用平截面假定确定钢筋应力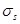
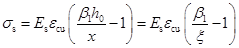 (6-32)
(6-32)
式中: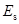 ——钢筋弹性模量;
——钢筋弹性模量;
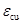 ——非均匀受压时的混凝土极限压应变,取0.0033;
——非均匀受压时的混凝土极限压应变,取0.0033;
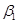 ——简化应力图形系数;
——简化应力图形系数;
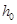 ——截面有效高度;
——截面有效高度;
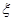 ——相对受压区高度
——相对受压区高度
(2)用经验公式确定钢筋应力(我国混凝土规范建议的方法)
式(6-30)表明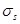 与
与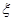 间呈双曲线型的函数关系,且如果
间呈双曲线型的函数关系,且如果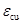 与
与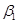 均不是定值,
均不是定值,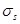 与
与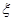 之间的关系将十分复杂,不便于计算。因而我国《混凝土规范》根据大量试验资料的统计分析,建议采用式(6-31)来确定
之间的关系将十分复杂,不便于计算。因而我国《混凝土规范》根据大量试验资料的统计分析,建议采用式(6-31)来确定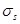 值。
值。
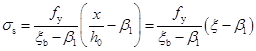 (6-33)
(6-33)
并且计算得到的钢筋应力应符合下列条件:
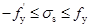 (6-34)
(6-34)
2. 基本计算公式
当全截面受压时,在一般情况下,靠近轴向力一侧的混凝土先被压碎,其实际应力图形和计算应力图形分别如图6-18(b)和6-18(c)所示。这时,受压区混凝土应力图形也可简化为矩形分布,其应力达到等效混凝土抗压强度设计值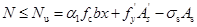 。靠近轴向力一侧的受压钢筋应力达到其抗压强度设计值,而离轴向力较远一侧的钢筋应力可能未达到其抗压强度设计值,也可能达到其抗压强度设计值。根据力的平衡条件和力矩平衡条件可得到小偏心受压构件正截面承载力的计算公式:
。靠近轴向力一侧的受压钢筋应力达到其抗压强度设计值,而离轴向力较远一侧的钢筋应力可能未达到其抗压强度设计值,也可能达到其抗压强度设计值。根据力的平衡条件和力矩平衡条件可得到小偏心受压构件正截面承载力的计算公式:
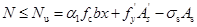 (6-35)
(6-35)
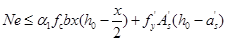 (6-36)
(6-36)
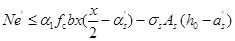 (6-37)
(6-37)
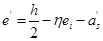 (6-38)
(6-38)
式中:x——受压区计算高度,当x>h时,计算时取x=h;
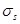 ——
——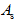 一侧钢筋应力值,可由式(6-31)求得;
一侧钢筋应力值,可由式(6-31)求得;
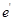 ——轴向力作用点至受压侧钢筋
——轴向力作用点至受压侧钢筋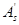 合力点之间的距离。
合力点之间的距离。