 学历课程
学历课程
文本一:偏心受拉构件正截面承载力计算
偏心受拉构件正截面承载力计算,按纵向拉力的作用位置不同,可以分为大偏心受拉与小偏心受拉两种情况:
(1)当纵向拉力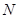 作用在钢筋
作用在钢筋 合力点和
合力点和 合力点范围之外时,为大偏心受拉;
合力点范围之外时,为大偏心受拉;
(2)当纵向拉力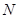 作用在钢筋
作用在钢筋 合力点和
合力点和 合力点范围之间时,为小偏心受拉。
合力点范围之间时,为小偏心受拉。
构件的大、小偏心受拉可以按下列公式进行判别:
(1)当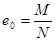 >
>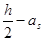 时,为大偏心受拉构件;
时,为大偏心受拉构件;
(2)当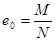 ≤
≤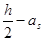 时,为小偏心受拉构件。
时,为小偏心受拉构件。
1. 大偏心受拉构件正截面承载力计算
大偏心受拉构件破坏时,混凝土虽开裂,但还有受压区,否则拉力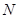 将得不到平衡。其破坏特征与
将得不到平衡。其破坏特征与 的数量有关,当
的数量有关,当 数量适当时,受拉钢筋首先屈服,然后受压钢筋的应力达到屈服强度,混凝土受压边缘达到极限应变而破坏,受压区混凝土强度达到
数量适当时,受拉钢筋首先屈服,然后受压钢筋的应力达到屈服强度,混凝土受压边缘达到极限应变而破坏,受压区混凝土强度达到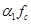 。
。
图7-1所示为矩形截面大偏心受拉构件计算图形。基本公式如下:
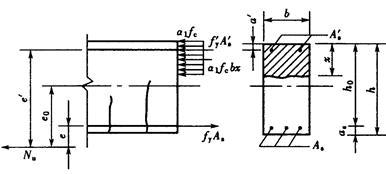
图7-1 矩形截面大偏心受拉构件计算图形
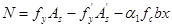 (7-2)
(7-2)
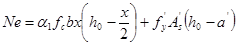 (7-3)
(7-3)
式中: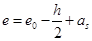 (7-4)
(7-4)
基本公式(7-2)和(7-3)的适用条件是: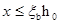 ,
,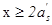 。
。
设计时为了使钢筋总用量( +
+ )最少,同偏心受压构件一样,应取
)最少,同偏心受压构件一样,应取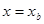 ,然后代入式(7-2)及式(7-3),可得
,然后代入式(7-2)及式(7-3),可得
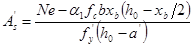 (7-5)
(7-5)
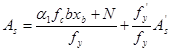 (7-6)
(7-6)
式中: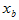 ——界限破坏时受压区的高度,
——界限破坏时受压区的高度,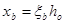 ,
,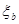 值可查表得到。
值可查表得到。
2. 小偏心受拉构件正截面承载力计算
小偏心受拉构件破坏时,一般情况下,全截面均为拉应力,其中 一侧的拉应力较大。随着荷载增加,
一侧的拉应力较大。随着荷载增加, 一侧的混凝土首先开裂,而且裂缝很快贯通整个截面,混凝土退出工作,拉力完全由钢筋承担,构件破坏时,
一侧的混凝土首先开裂,而且裂缝很快贯通整个截面,混凝土退出工作,拉力完全由钢筋承担,构件破坏时, 和
和 都达到屈服强度,截面受拉计算图形见图7-3。在这种情况下,不考虑混凝土的受拉作用。设计时,可假定构件破坏时钢筋
都达到屈服强度,截面受拉计算图形见图7-3。在这种情况下,不考虑混凝土的受拉作用。设计时,可假定构件破坏时钢筋 及
及 的应力都达到屈服强度。根据内外力分别对钢筋
的应力都达到屈服强度。根据内外力分别对钢筋 及
及 的合力点取矩的平衡条件,可得
的合力点取矩的平衡条件,可得
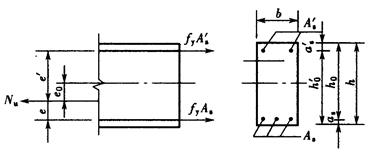
图7-3 小偏心受拉计算图形
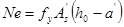 (7-9)
(7-9)
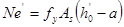 (7-10)
(7-10)
式中:
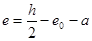 (7-11)
(7-11)
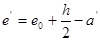 (7-12)
(7-12)