9.3.1 变形控制的要求

对于适用性和耐久性，结构构件满足正常使用要求的限值大都凭长期使用经验确定，《混凝土规范》规定了各种情况下变形的限值。

对于受弯构件，挠度变形的验算表达式为：

　　　　　　　　　　　　(9-23)

式中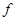：——荷载作用产生的挠度变形；

　　　——挠度变形限值。

9.3.2 截面抗弯刚度的主要特点（视频与第9.3.1节相同）

由材料力学可知，均质弹性体梁满足下列条件：（1）物理条件——应力与应变满足虎克定律；（2）几何条件——平截面假定；（3）平衡条件——钢筋混凝土构件中钢筋屈服前变形的计算。材料力学中已给出线弹性体梁跨中最大挠度的一般公式为：

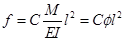　　　　　　　　　　　　(9-24)

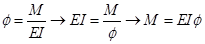　　　　　　　　　　　　(9-25)

以上述3个条件为基础，并在物理条件中考虑混凝土受压的非线性。当截面及材料给定后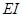，为常数，即挠度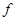与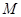为直线关系，如图9-8中虚线所示。

加载到破坏实测的混凝土适筋梁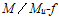关系曲线如图9-8实线所示，钢筋混凝土受弯构件的刚度不是一个常数，裂缝的出现与开展对其有显著影响。对普通钢筋混凝土受弯构件来讲，在使用荷载作用下，绝大多数处于第二阶段，因此，正常使用阶段的变形验算，主要是指这一阶段的变形验算。另外，试验还表明，截面刚度随时间的增长而减小。所以，在普通钢筋混凝土受弯构件的变形验算中，除考虑荷载效应准永久组合以外，还应考虑荷载长期作用的影响。受弯构件的截面刚度记为B，受弯构件在荷载效应准永久组合下的刚度（短期刚度）记为。

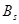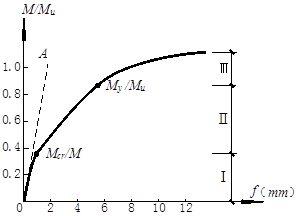
图 9-8 适筋梁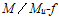曲线

由于混凝土的不均匀性，各截面混凝土的实际抗拉强度存在差异，随着荷载的增加，在某一最薄弱的截面上将出现第一条裂缝（如图9-1所示的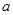-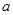截面），有时也可能在几个截面上同时出现一批裂缝。在裂缝截面上的混凝土不再承受拉力，这部分拉力转由钢筋来承担，钢筋应力将突然增大，应变也突增。加上原来受拉伸长的混凝土应力释放后又瞬间产生回缩，所以裂缝一出现就会有一定的宽度。

9.3.3 短期刚度计算公式（视频与第9.3.1节相同）

1、使用阶段受弯构件的应变分布特征

钢筋混凝土受弯构件变形计算是以适筋梁第Ⅱ阶段应力状态为计算依据。取梁的纯弯曲段来研究其应力、应变特点。由试验可知，在第Ⅱ阶段，从裂缝出现到裂缝稳定，沿构件的长度方向应力和应变分布如图9-9所示，具有以下特点：

（1）钢筋应变沿梁长分布不均匀，裂缝截面处应变较大，裂缝之间应变较小。其不均匀程度可以用受拉钢筋应变不均匀系数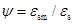来反映。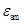为裂缝间钢筋的平均应变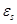，为裂缝截面处的钢筋应变。所以有：

　　　　　　　　　　　　(9-26)

（2）压区混凝土的应变沿梁长分布也是不均匀的。裂缝截面处应变较大，裂缝之间应变较小。则可得：

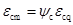　　　　　　　　　　　　(9-27)

（3）由于裂缝的影响，截面中和轴的高度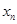也呈波浪形变化，开裂截面处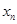小而裂缝之间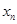较大。其平均值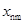称为平均中和轴高度，相应的中和轴为平均中和轴，相应截面称为平均截面，相应曲率为平均曲率，平均曲率半径记为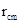。试验表明，平均应变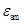、符合平截面假定，即沿平均截面平均应变呈直线分布。

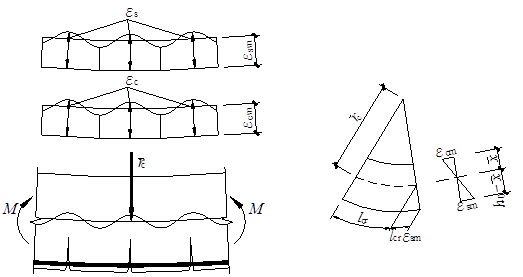
图 9-9 钢筋混凝土梁纯弯段的应变分布

2、钢筋混凝土受弯构件的短期刚度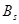

在梁的纯弯段内，其平均应变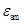、符合平截面假定。仍可采用材料力学中匀质弹性体曲率相似的公式．即：

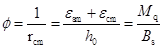　　　　　　　　　　　　(9-28)

式中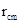：为平均曲率半径。

利用弯矩曲率关系，可求得受弯构件的短期刚度：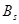

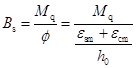　　　　　　　　　　　　(9-29)

钢筋平均应变与裂缝截面钢筋应力的关系为：

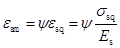　　　　　　　　　　　　(9-30)

另外，由于受压区混凝土的平均应变与裂缝截面的应变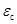相差很小，再考虑到混凝土的塑性变形而采用的变形模量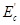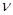（，为弹性系数），则

　　　　　　　　　　　　(9-31)

裂缝截面的实际应力分布如图9-10所示，计算时可把混凝土受压应力图取作等效矩形应力图形，并取平均应力为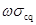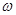，为压应力图形系数。

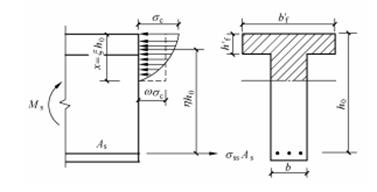
图 9-10 裂缝截面计算图形

设裂缝截面受压区高度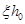，截面的内力臂为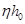。由图9-10所示，对受压区合力作用点取矩，可得：

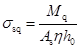　　　　　　　　　　　　(9-32)

受压区面积为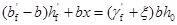，将曲线分布的压应力图形换算成平均压应力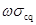，再对受拉钢筋的重心处取矩，则得：

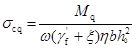　　　　　　　　　　　　(9-33)

式中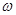：——压应力图形丰满程度系数；

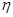　　　——裂缝截面处内力臂长度系数；

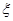　　　——裂缝截面处受压区高度系数；

　　　——受压翼缘的加强系数，。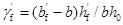

综合上述3项关系，即可得到：

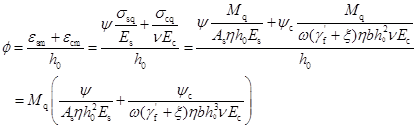　　　　　　　　　　　　(9-34)

上式即为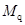与曲率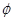的关系式。设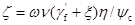，并称为混凝土受压边缘平均应变综合系数。经整理，可得短期刚度的表达式：

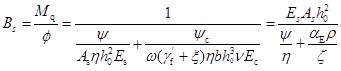　　　　　　　　　　　　(9-35)

式中，，

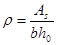
试验表明，受压区边缘混凝土平均应变综合系数随荷载增大而减小，在裂缝出现后降低很快，而后逐渐减缓，在使用荷载范围内则基本稳定。因此，的取值可不考虑荷载的影响。根据试验资料统计分析可得

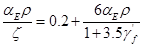　　　　　　　　　　　　(9-36)

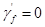式中——受压翼缘加强系数，对于矩形截面，；对与T形截面当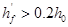时，取。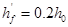

将式（9-36）带入式（9-35），则受弯构件短期刚度公式可写为：

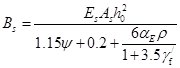　　　　　　　　　　　　(9-37)

式中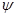：参照式（9-19）进行计算。

9.3.4 长期刚度计算公式

在荷载长期作用下，受压区混凝土将发生徐变，裂缝间仍处于受拉状态，裂缝附近混土的应力松弛以及它与钢筋间的滑移使受拉混凝土不断退出工作，因而钢筋应变随时间而增大。此外，由于纵向受拉钢筋周围混凝土的收缩受到钢筋的抑制，当受压纵向钢筋用量较少时，受压区混凝土可较自由地收缩变形，梁产生弯曲使梁的刚度降低，导致梁挠度增长。

荷载长期作用下挠度增长的主要原因是混凝土的徐变和收缩，因此，凡是影响混凝土徐变和收缩的因素：如受压钢筋的配筋率、加载龄期、温度、湿度及养护条件等，都对长期挠度有影响。

试验表明，在加载初期，梁的挠度增长较快，随后，在荷载长期作用下，其增长趋势逐渐减缓，后期挠度虽继续增长，但增值很小。实际应用中，对一般尺寸的构件，可取1000天或3年挠度作为最终值。对于大尺寸构件，挠度增长在10年后仍未停止。

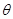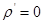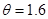《混凝土规范》通过试验确定钢筋混凝土受弯构件的挠度增大系数，来计算荷载长期影响的刚度。当时，；当时，；当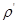为中间数值时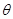，按线性内插法取用。此处，。

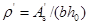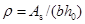上述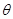值适用于一般情况下的矩形、T形和I形截面梁。由于值与温湿度有关，对于干燥地区，收缩影响大，由此建议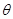应酌情增加15%~20%。对翼缘位于受拉区的倒T形截面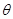，应增加20%。

根据国内的试验分析结果，受压钢筋对荷载短期作用下挠度影响较小，但对荷载长期作用下受压区混凝土徐变以至梁的挠度增长起着抑制作用。抑制程度与受压钢筋和受拉钢筋的相对数量有关，并且对早龄期的梁，受压钢筋对减小梁的挠度作用大些。

《混凝土规范》给出普通钢筋混凝土构件按荷载准永久组合并考虑长期作用影响的矩形、T形、倒T形和工字形截面受弯构件的刚度计算公式，如下：

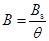　　　　　　　　　　　　(9-38)

式中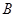：——按荷载效应的准永久组合并考虑荷载长期作用影响的刚度；

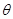　　　——考虑荷载长期作用对挠度增大的影响系数；

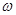　　　——荷载效应的准永久组合作用下受弯构件的短期刚度。

9.3.5 最小刚度原则（视频与第9.3.4节相同）

式（9-37）及式（9-41）都是指纯弯区段内平均的截面弯曲刚度，但就一般受弯构件而言，在其跨度范围内各截面的弯矩一般是不相等的，故各截面弯曲刚度也不相同。实际应用中为了简化计算，常采用同一符号弯矩区段内最大弯矩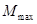处的截面刚度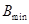作为该区段的刚度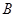以计算构件的挠度，这就是受弯构件挠度计算中的“最小刚度原则”。

对于简支梁，根据“最小刚度原则”，可按梁全跨范围内弯矩最大处的截面弯曲刚度，亦即最小的截面弯曲刚度[如图9-11（b）中虚线所示]，用结构力学方法中不考虑剪切变形影响的等截面梁公式来计算挠度。对于等截面连续梁，存在正、负弯矩，可假定各同一符号弯矩区段内的刚度相等，并分别取正、负弯矩区段处截面的最小刚度按变刚度连续梁计算挠度。当计算跨度内的支座截面弯曲刚度不大于跨中截面弯曲刚度的2倍或不小于跨中截面弯曲刚度的1/2时，该跨也可按等刚度构件进行计算，且其构件刚度可取跨中最大弯矩截面的弯曲刚度。

采用“最小刚度原则”表面上看会使挠度计算值偏大，但由于计算中多不考虑剪切变形及其裂缝对挠度的贡献，两者相比较，误差大致可以互相抵消。对国内外约350根试验梁验算结果表明，计算值与试验值符合较好。因此，采用“最小刚度原则”可以满足工程要求。用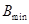代替匀质弹性材料梁截面弯曲刚度EI后，梁的挠度计算十分简便。

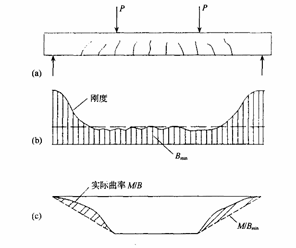
图9-11 简支梁沿梁长的刚度和曲率分布