 学历课程
学历课程
文本一:双筋矩形截面正截面受弯承载力计算
4.6.1 双筋矩形截面的受力机理
什么情况下需要考虑采用双筋截面梁?
情况一:当给定的弯矩设计值过大,此时按单筋梁进行截面设计不能满足适筋梁的适用条件(),且由于使用要求,截面高度受到限制又不能增大,同时混凝土强度等级因条件限制不能再提高时,可采用双筋截面。即在截面的受压区配置纵向钢筋以补充混凝土受压能力的不足。
情况二:对于在水平荷载作用下的框架梁,当其在地震或风等往复荷载作用下,同一截面上会产生反向弯矩。为了承受往复弯矩分别作用时截面顶部和底部均可能出现的拉力,需在截面的顶部和底部均配置纵向钢筋,因而形成了双筋截面。此外,受压钢筋的存在可提高截面的延性,因此,抗震设计中要求框架梁截面上部和下部必须配置一定比例的纵向钢筋。
双筋截面梁的受力特点?双筋截面可以理解为在单筋截面的基础上通过成对增加拉压区配筋形成力偶来增加截面的受弯承载力。双筋梁在满足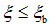 的条件下仍然具有适筋梁的塑性破坏特征,即受拉钢筋首先屈服,然后经历一个充分的变形过程,受压区混凝土才被压碎。因此,在进行抗弯承载力计算时,受压区混凝土仍可采用等效矩形应力图形和换算的弯曲抗压设计强度
的条件下仍然具有适筋梁的塑性破坏特征,即受拉钢筋首先屈服,然后经历一个充分的变形过程,受压区混凝土才被压碎。因此,在进行抗弯承载力计算时,受压区混凝土仍可采用等效矩形应力图形和换算的弯曲抗压设计强度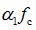 。
。
双筋截面梁的构造要求?试验表明,受压钢筋在纵向压力作用下易产生压曲而导致侧向凸出,并将受压区保护层崩裂使构件提前发生破坏,降低构件的承载力。为防止受压纵筋压曲和侧向凸出,必须在梁内布置封闭箍筋对其进行约束,受压钢筋才能与受压混凝土共同变形和受力,直到混凝土压碎破坏。
4.6.2 基本计算公式
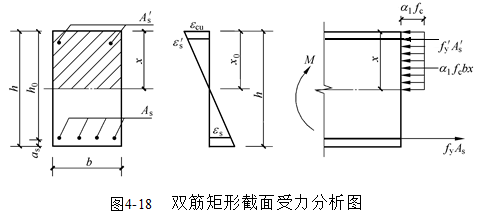
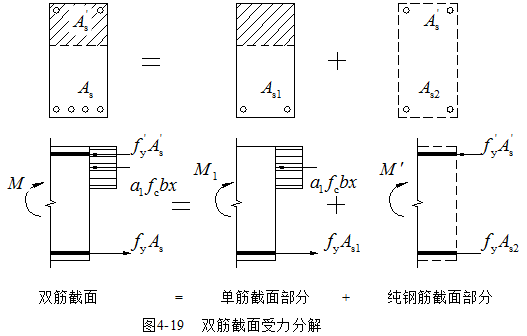
考虑受压钢筋参加工作,可以得出如图4-18所示的双筋矩形截面抗弯承载力计算的应力图,并可分解为图4-19所示的单筋截面部分和纯钢筋截面部分。由平衡条件可写出以下基本公式
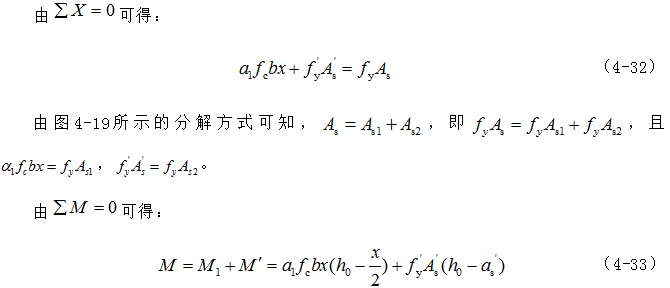
式中: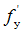 ——钢筋的抗压设计强度;
——钢筋的抗压设计强度;
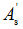 ——受压钢筋的截面面积;
——受压钢筋的截面面积;
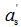 ——受压钢筋的合力点到截面受压边缘的距离;
——受压钢筋的合力点到截面受压边缘的距离;
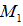 ——压区混凝土与部分受拉钢筋
——压区混凝土与部分受拉钢筋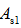 所提供的相当于单筋矩形截面的受弯承载力,
所提供的相当于单筋矩形截面的受弯承载力,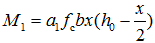 (4-34)
(4-34)
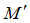 ——受压钢筋
——受压钢筋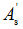 与部分受拉钢筋
与部分受拉钢筋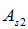 所提供的受弯承载力,
所提供的受弯承载力,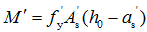 (4-35)
(4-35)
其它符号同单筋矩形截面梁的分析。
以上基本公式的适用条件和单筋矩形截面梁计算公式的适用条件相同:
(1)防止出现超筋破坏,应满足
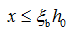 (4-36)
(4-36)
(2)为保证受压钢筋达到规定的抗压设计强度,应满足
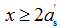 (4-37)
(4-37)
4.6.3 双筋矩形截面正截面受弯承载力的截面设计方法
1、截面设计(包括两种情况)
(1)已知设计弯矩M,材料强度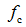 ,
, 及
及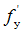 和截面尺寸b,h,要求确定所需的受压和受拉钢筋,即
和截面尺寸b,h,要求确定所需的受压和受拉钢筋,即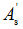 和
和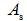 。
。
计算步骤:
(1)判明是否需要配置受压钢筋
计算单筋矩形截面充分增加配筋后所能发挥的最大抗弯能力: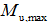
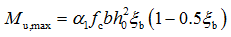
如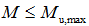 ,说明不需要配置受压钢筋,可按单筋矩形截面计算
,说明不需要配置受压钢筋,可按单筋矩形截面计算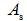 ;
;
如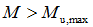 ,说明计算上需要配置受压钢筋。
,说明计算上需要配置受压钢筋。
(2)分别计算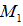 和
和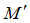
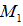 是指混凝土充分利用时合力形成的力偶
是指混凝土充分利用时合力形成的力偶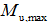 ,即
,即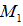 =
=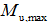 ,则受压钢筋产生的力偶
,则受压钢筋产生的力偶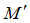 =
=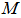 -
-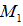 。
。
(3)计算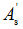 和
和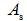
受压钢筋面积: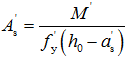 ;
;
总的受拉钢筋面积为: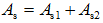 ;
;
根据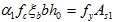 ,得到
,得到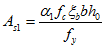 ;
;
根据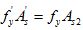 ,得到
,得到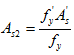 。
。
(2)已知设计弯矩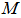 ,截面尺寸b,h,材料强度等级
,截面尺寸b,h,材料强度等级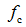 ,及
,及 和
和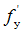 受压钢筋面积
受压钢筋面积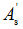 ,要求确定受拉钢筋面积
,要求确定受拉钢筋面积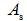 。
。
计算步骤:
(1)这种情况下,为了使总用钢量最小,首先利用已经给定的受压钢筋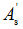 进行计算。
进行计算。
假定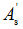 可达到屈服强度,其所提供的抗弯承载力为
可达到屈服强度,其所提供的抗弯承载力为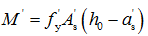 ,设计弯矩值中的其余部分应由混凝土受压区和部分受拉纵筋提供,故
,设计弯矩值中的其余部分应由混凝土受压区和部分受拉纵筋提供,故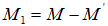 。
。
(2)计算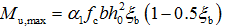 ,如
,如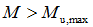 ,说明给定的
,说明给定的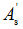 尚不足,需按
尚不足,需按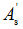 未知的第(1)种情况计算
未知的第(1)种情况计算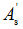 及
及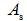 ;如
;如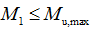 ,令
,令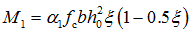 求得
求得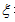 及
及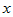 受压区高度,进一步求出
受压区高度,进一步求出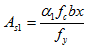 。注意,这时应验算条件
。注意,这时应验算条件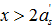 。
。
(3)计算全部受拉钢筋面积,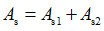 ,其中
,其中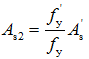 。
。
注意:如果受压区高度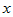 小于
小于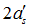 ,表明受压区钢筋未达到屈服,此时应按式(4-38)计算
,表明受压区钢筋未达到屈服,此时应按式(4-38)计算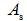 ,即
,即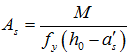 。
。
2、截面复核
已知截面尺寸b、h,材料强度等级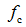 ,
, ,
,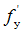 和钢筋用量
和钢筋用量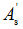 及
及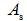 ,要求复核截面的抗弯承载力。
,要求复核截面的抗弯承载力。
计算步骤:
(1)首先按照受压钢筋能够达到屈服的情况计算。利用公式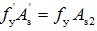 求出
求出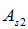 ,利用公式
,利用公式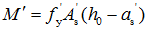 计算出相应的
计算出相应的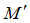 。
。
2)由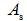 减去
减去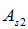 得
得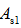 ,然后按复核单筋截面的同样步骤求得
,然后按复核单筋截面的同样步骤求得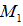 。将
。将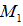 与
与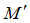 相加即可得出截面所能承担的弯矩
相加即可得出截面所能承担的弯矩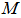 。
。
注意:若算得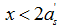 ,则应改按公式
,则应改按公式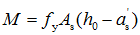 计算截面所能承担的弯矩;若出现
计算截面所能承担的弯矩;若出现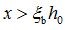 的情况,说明截面已属超筋,可近似用公式
的情况,说明截面已属超筋,可近似用公式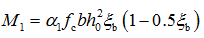 来计算。
来计算。
3、典型例题