 学历课程
学历课程
文本一:矩形截面不对称配筋偏心受压构件的计算方法
6.6.1 截面设计
1. 大偏心受压构件的截面计算
在已知截面尺寸(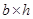 )、材料强度(
)、材料强度(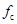 、
、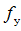 、
、 )、构件长细比(
)、构件长细比(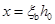 )以及轴力N和弯矩M的设计值的情况下,当
)以及轴力N和弯矩M的设计值的情况下,当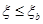 时,一般可先按大偏心受压情况计算纵向钢筋
时,一般可先按大偏心受压情况计算纵向钢筋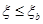 和
和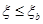 。此时设计基本计算公式:
。此时设计基本计算公式:
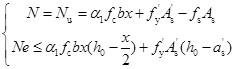 (6-39)
(6-39)
式中: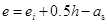
(1)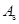 和
和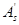 均未知时,基本方程中有3个未知数,无解。与双筋截面类似,使(
均未知时,基本方程中有3个未知数,无解。与双筋截面类似,使(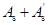 )最小,可以取
)最小,可以取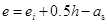 ,带入式(6-39)可得:
,带入式(6-39)可得:
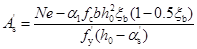 (6-40)
(6-40)
若上式求得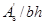 小于受压钢筋的最小配筋率0.002,则应取
小于受压钢筋的最小配筋率0.002,则应取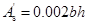 ,然后按照
,然后按照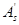 已知计算。
已知计算。
将求得的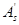 和
和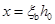 带入(6-39)式,可得:
带入(6-39)式,可得:
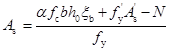 (6-41)
(6-41)
若按上式求得的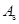 小于
小于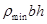 取
取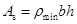 。
。
(2)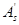 为已知时,基本方程的未知数为两个,即
为已知时,基本方程的未知数为两个,即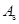 与
与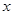 ,方程有唯一解,这时应先由(6-39)式求解
,方程有唯一解,这时应先由(6-39)式求解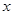 ,若计算
,若计算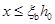 ,且
,且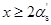 ,则可用下式求解出
,则可用下式求解出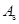 :
:
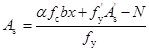 (6-42)
(6-42)
若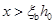 ,则应按
,则应按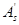 未知的情况重新计算
未知的情况重新计算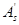 ;若
;若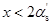 ,则可偏于安全取
,则可偏于安全取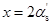 ,对
,对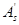 合力中心取矩后,按教材式(6-29)确定
合力中心取矩后,按教材式(6-29)确定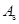 。
。
以上求得的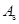 若小于
若小于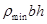 ,则截面为小偏心受压,取
,则截面为小偏心受压,取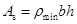 进行小偏压设计。当然,也可按
进行小偏压设计。当然,也可按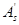 为已知的双筋梁的计算方法进行计算,但计算中应将
为已知的双筋梁的计算方法进行计算,但计算中应将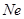 用
用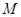 代换。
代换。
2. 小偏心受压构件的截面计算
在进行小偏心受压构件(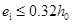 )截面设计时,由式(6-35)、式(6-36)或式(6-37)可知,共有3个未知数
)截面设计时,由式(6-35)、式(6-36)或式(6-37)可知,共有3个未知数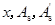 ,两个独立方程,故需补充一个条件才能求解。由于小偏心受压构件破坏时,远离轴向力一侧的钢筋应力通常小于其强度设计值,所以,为了节约钢材,可先按最小配筋率
,两个独立方程,故需补充一个条件才能求解。由于小偏心受压构件破坏时,远离轴向力一侧的钢筋应力通常小于其强度设计值,所以,为了节约钢材,可先按最小配筋率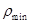 及构造要求假定
及构造要求假定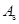 ,即:
,即:
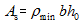
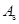 值确定后,即可求得
值确定后,即可求得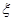 (或
(或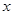 )和
)和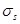 ,若
,若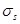 < 0,取
< 0,取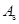 =
=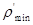
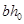 ,然后用式(6-37)及式(6-33)重新求得
,然后用式(6-37)及式(6-33)重新求得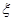 。根据解得的
。根据解得的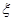 可分为以下3种情况:
可分为以下3种情况:
(1)若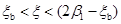 ,则按式(6-35)求得的
,则按式(6-35)求得的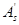 即为所求受压钢筋面积,计算完毕。
即为所求受压钢筋面积,计算完毕。
(2)若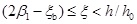 ,此时
,此时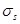 达到
达到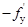 ,计算时,取
,计算时,取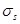 =
=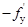 ,
,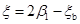 ,通过式(6-35)、式(6-36)可求得
,通过式(6-35)、式(6-36)可求得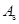 及
及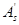 。
。
(3)若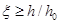 ,则为全截面受压,此时应取,
,则为全截面受压,此时应取,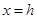 ,
,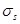 =
=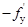 并代入式(6-35)、式(6-36)计算
并代入式(6-35)、式(6-36)计算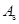 及
及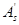 。
。
对于(2)和(3)两种情况,均应再复核反向破坏的承载力,并且保证计算所得的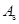 ,
,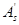 值满足最小配筋率的要求,即
值满足最小配筋率的要求,即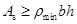 ,
,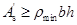 。
。
6.6.2 截面复核
复核截面的承载能力也是经常遇到的问题。此时一般已知构件的计算长度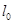 ,截面尺寸、材料强度及截面配筋,要求计算截面所能承受的轴向力
,截面尺寸、材料强度及截面配筋,要求计算截面所能承受的轴向力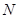 及弯矩
及弯矩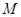 。由于
。由于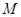 =
=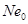 ,所以截面复核实际上有两种情形:已知轴向力设计值
,所以截面复核实际上有两种情形:已知轴向力设计值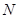 ,求截面能承受的弯矩设计值
,求截面能承受的弯矩设计值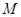 或偏心距
或偏心距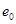 ;或者已知平面弯矩设计值
;或者已知平面弯矩设计值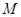 ,验算截面能否承受该轴向力
,验算截面能否承受该轴向力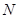 值。
值。
1.弯矩作用平面的承载力复核
(1)给定轴向力设计值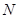 ,求弯矩作用平面的弯矩设计值
,求弯矩作用平面的弯矩设计值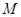
由于给定的截面尺寸、配筋和材料强度均已知,故未知数有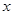 ,
,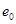 和
和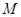 共3个。
共3个。
先将已知配筋量和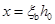 代入式(6-24)求得界限轴向力
代入式(6-24)求得界限轴向力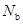 。
。
如果给定的轴向力设计值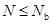 ,则为大偏心受压,可按式(6-24)重新求解
,则为大偏心受压,可按式(6-24)重新求解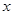 ;如果求得的
;如果求得的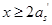 ,则将
,则将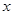 代入式(6-25)求解
代入式(6-25)求解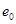 ;如果求得的
;如果求得的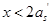 ,则取
,则取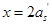 ,利用式(6-29)求解
,利用式(6-29)求解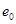 ,弯矩设计值
,弯矩设计值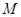 =
=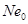 。
。
如果给定的轴向力设计值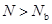 ,则为小偏心受压,按式(6-33)和式(6-35)求解
,则为小偏心受压,按式(6-33)和式(6-35)求解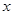 ,再将
,再将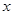 代入式(6-36)求解
代入式(6-36)求解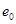 及
及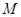 。
。
(2)给定轴向力作用的偏心距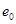 ,求轴向力设计值
,求轴向力设计值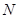
此时的未知数为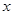 和
和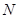 两个,因截面配筋已知,故可先按大偏心受压情况,对轴向力
两个,因截面配筋已知,故可先按大偏心受压情况,对轴向力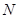 作用点取矩,根据力平衡条件得
作用点取矩,根据力平衡条件得
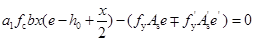 (6-47)
(6-47)
式中,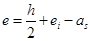 ,
,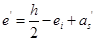 。
。
由式(6-47)可求得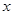 ,若求出的
,若求出的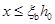 时,为大偏心受压,若同时
时,为大偏心受压,若同时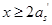 ,即可将
,即可将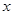 代入式(6-24)求截面能承受的轴向力
代入式(6-24)求截面能承受的轴向力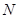 。
。
若求出的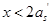 ,则按式(6-29)求截面能承受的轴向力
,则按式(6-29)求截面能承受的轴向力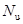 。
。
若求出的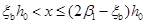 ,则为小偏心受压,可将已知数据代入式(6-33)、 式(6-35)和式(6-36)联立求解
,则为小偏心受压,可将已知数据代入式(6-33)、 式(6-35)和式(6-36)联立求解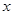 以及截面能承受的轴向力
以及截面能承受的轴向力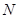 。
。
若求出的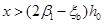 ,则取
,则取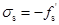 ,然后按式(6-35)、式(6-36)重新求解
,然后按式(6-35)、式(6-36)重新求解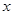 及
及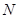 ,同时还应考虑
,同时还应考虑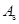 一侧混凝土可能先压坏的情况,所以应按下式来求解轴向力
一侧混凝土可能先压坏的情况,所以应按下式来求解轴向力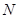 :
:
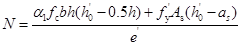 (6-48)
(6-48)
式中: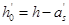 ,
,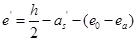
式(6-48)与式(6-35)求得的轴向力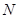 比较后,取较小的值作为轴向力设计值。
比较后,取较小的值作为轴向力设计值。
2. 垂直于弯矩作用平面的承载力计算
除了在弯矩作用平面内依照偏心受压进行计算外,当构件在垂直于弯矩作用平面内的长细比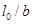 较大时,尚应根据
较大时,尚应根据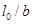 确定稳定系数
确定稳定系数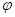 ,按轴心受压情况验算垂直于弯矩作用平面的受压承载力,并与上面求得的
,按轴心受压情况验算垂直于弯矩作用平面的受压承载力,并与上面求得的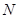 比较后,取较小值。
比较后,取较小值。