 学历课程
学历课程
第三节:纯扭构件承载力的计算
计算原则:纯扭构件在裂缝出现前,构件内纵筋和箍筋的应力都很小,因此当扭矩不足以使构件开裂时,按构造要求配置受扭钢筋即可。当扭矩较大致使构件形成裂缝后,此时需按计算配置受扭纵筋及箍筋,以满足构件的承载力要求。扭曲截面承载力计算中,构件开裂扭矩的大小决定了受扭构件的钢筋配置是否仅按构造配置或者需由计算确定。
8.3.1 开裂扭矩
根据试验结果,由于钢筋混凝土纯扭构件在裂缝出现前的钢筋应力很小,钢筋的存在对开裂扭矩的影响也不大,所以构件截面开裂扭矩的确定可以忽略钢筋的作用。
为实用方便起见,根据大量试验的结果,我们将按理想弹塑性材料计算的开裂扭矩乘以0.7的降低系数,作为混凝土材料开裂扭矩的计算公式:
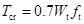 (8-1)
(8-1)
式中: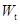 为受扭构件的截面受扭塑性抵抗矩。
为受扭构件的截面受扭塑性抵抗矩。
8.3.2 纯扭构件的承载力
试验表明,受扭的素混凝土构件,一旦出现斜裂缝即完全破坏。若配置适量的受扭纵筋和受扭箍筋,则不但其承载力有较显著的提高,且构件破坏时会具有较好的延性。
通过对钢筋混凝土矩形截面纯扭构件的试验研究和统计分析,在满足可靠度要求的前提下,提出如下半经验半理论的纯扭构件承载力计算公式。
1、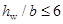 矩形截面钢筋混凝土纯扭构件受扭承载力计算公式
矩形截面钢筋混凝土纯扭构件受扭承载力计算公式
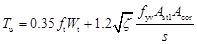 (8-2)
(8-2)
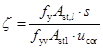 (8-3)
(8-3)
式中: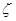 ——受扭纵向钢筋与箍筋的配筋强度比;
——受扭纵向钢筋与箍筋的配筋强度比;
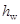 ——截面的腹板高度:对矩形截面,取有效高度
——截面的腹板高度:对矩形截面,取有效高度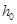 ;
;
式(8-2)由两项组成:第一项为开裂混凝土承担的扭矩,第二项为钢筋承担的扭矩,是建立在适筋破坏形式的基础上的。
系数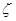 为受扭纵向钢筋与箍筋的配筋强度比,用来考虑纵筋与箍筋不同配筋比和不同强度比对受扭承载力的影响,以避免某一种钢筋配置过多形成部分超筋破坏。试验表明,若
为受扭纵向钢筋与箍筋的配筋强度比,用来考虑纵筋与箍筋不同配筋比和不同强度比对受扭承载力的影响,以避免某一种钢筋配置过多形成部分超筋破坏。试验表明,若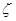 在0.5~2.0内变化,构件破坏时,其受扭纵筋和箍筋应力均可达到屈服强度。为稳妥见,取
在0.5~2.0内变化,构件破坏时,其受扭纵筋和箍筋应力均可达到屈服强度。为稳妥见,取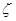 的限制条件为
的限制条件为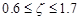 ,当
,当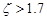 时,按
时,按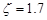 计算。
计算。
对于在轴向压力和扭矩共同作用下的矩形截面钢筋混凝土构件,其受扭承载力应按下列公式计算:
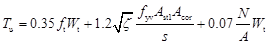 (8-4)
(8-4)
式中: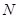 ——与扭矩设计值
——与扭矩设计值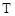 对应的轴向压力设计值,当
对应的轴向压力设计值,当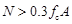 时,取
时,取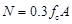 。
。
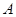 ——构件截面面积。
——构件截面面积。
2、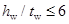 的箱形截面钢筋混凝土纯扭构件受扭承载力计算公式
的箱形截面钢筋混凝土纯扭构件受扭承载力计算公式
实验和理论研究表明,一定壁厚箱形截面的受扭承载力与相同尺寸的实心截面构件是相同的。对于箱形截面纯扭构件,采用下列计算公式:
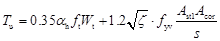 (8-5)
(8-5)
式中,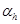 ——箱型截面壁厚影响系数;
——箱型截面壁厚影响系数;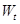 ——箱形截面受扭塑性抵抗矩。
——箱形截面受扭塑性抵抗矩。
3、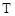 形和
形和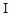 形截面纯扭构件的受扭承载力计算公式
形截面纯扭构件的受扭承载力计算公式
对于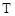 形和
形和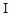 形截面,可将其截面划分为几个矩形截面进行配筋计算,矩形截面划分的原则是首先满足腹板截面的完整性,然后再划分受压翼缘和受拉翼缘的面积,如图8-4所示。划分的各矩形截面所承担的扭矩值,按各矩形截面的受扭塑性抵抗矩与截面总的受扭塑性抵抗矩的比值进行分配的原则确定,并分别按式(8-2)计算受扭承载力。
形截面,可将其截面划分为几个矩形截面进行配筋计算,矩形截面划分的原则是首先满足腹板截面的完整性,然后再划分受压翼缘和受拉翼缘的面积,如图8-4所示。划分的各矩形截面所承担的扭矩值,按各矩形截面的受扭塑性抵抗矩与截面总的受扭塑性抵抗矩的比值进行分配的原则确定,并分别按式(8-2)计算受扭承载力。
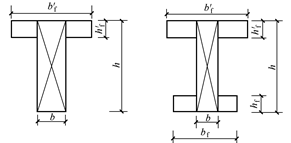
图8-4 形和形截面的矩形划分方法